In my job as a data analyst, I come across many different types of problems to solve. Some are relatively easy to solve, others not so much. That was until recently, where I came across a problem I have never given much thought before. That was until now.
What is the problem? Finding multiple peaks in a dataset.
You might think, this sounds incredibly simple. Just take the max value in the set. And sure, you would be right. While this is ideal for finding the global maximum, it doesn’t cover all peaks. Note, I’m using the plural, implying multiple peaks.
The Problem
Let me explain this further with some dummy data. Consider the simple function below.
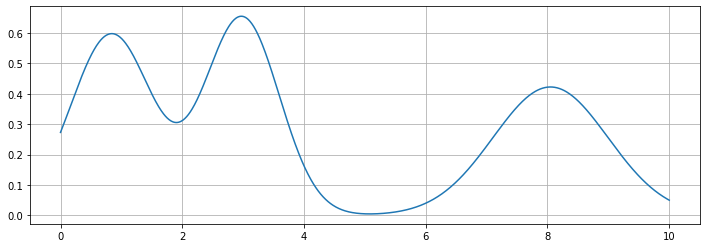
It’s quite clear from the graphic that there are three distinct peaks in the dataset where some are higher than others.
If we were to take the argmax (finding the max value’s index position), we would end up finding the global maximum.
However, as you can see, there are multiple peaks in this set. What if I wanted to find the locations for each of these three peaks?
This is where we counter our first issue with the argmax function.
Problem 1: argmax can only find the highest peak.
So with this in mind, our second option might be to use the argmax function to take the index of not just the highest value, but the second and third-highest values in the set by taking the top N (N, being some fixed number) sorted values.
This is what it would look like if the top three values were plotted on the same dataset.
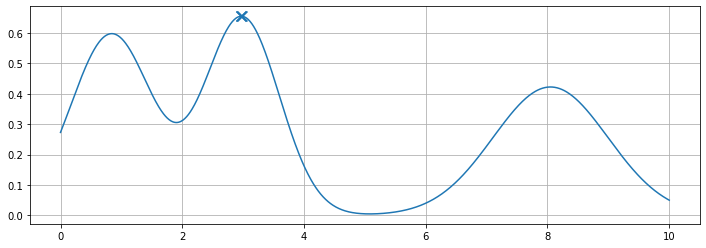
As you can see, this reveals another issue with argmax as the three values selected are piled around the largest peak. This because the second and third-highest values in the set are still found within the highest peak.
It only finds the peaks closest to each other, even though it’s clear that there are other peaks.
Problem 2: argmax can’t detect multiple peaks
So this raises an important question.
“How can we adequately detect multiple peaks in a dataset?“
To answer this, we need to consider things such as distance between peaks, peak height, thresholds and neighbouring values.
The Solution
Thankfully, If you live in the world of Python like me, then you are in luck. Using the awesome scipy package, there is a function known as find_peaks which does the job for us.
I won’t go into the maths in detail but, according to scipy “a peak or local maximum is defined as any sample whose two direct neighbours have a smaller amplitude“.
Revisiting our example earlier, using the find_peaks algorithm correctly finds all the peaks as marked below.
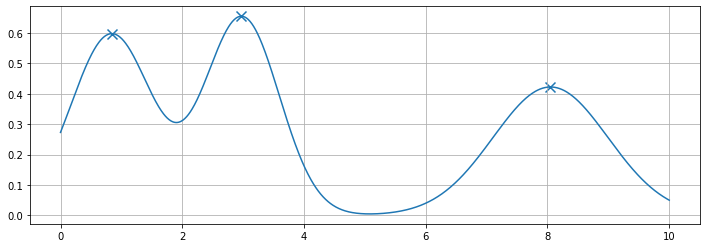
Here is an example snippet of how this can be implemented in Python. In my case, I built my own my fancy peak creator function, which essentially combines three normal distributions using random values for location and scale.
